Repita el siguiente conjunto de reglas hasta que no se puedan añadir mas símbolos terminales o a ningún conjunto ![]() :
:
-
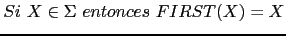
-

-
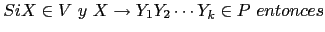
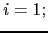

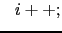
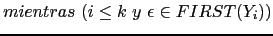
- Añadir
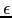 a
a 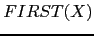 si
si 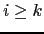 y
y



Repita el siguiente conjunto de reglas hasta que no se puedan añadir mas símbolos terminales o a ningún conjunto ![]() :
:
Este algoritmo puede ser extendido para calcular
![]() para
para
![]() .
El esquema es anólogo al de un símbolo individual.
.
El esquema es anólogo al de un símbolo individual.
Repita siguiente conjunto de reglas hasta que no se puedan añadir mas
símbolos terminales o a ningún conjunto
![]() :
:
Repetir los siguientes pasos hasta que ninguno de los conjuntos ![]() cambie:
cambie:

