Sig: Árbol de Análisis Abstracto Sup: Recursión por la Izquierda Ant: Ejercicio Err: Si hallas una errata ...

Práctica: Eliminación de la Recursividad por la Izquierda

En esta práctica vamos a extender las fases de análisis léxico y sintáctico del compilador del lenguaje Tutu cuya gramática se definió en el ejercicio 4.5.1 con expresiones que incluyen diferencias y divisiones. Además construiremos una representación del árbol sintáctico concreto. Para ello consideremos el siguiente esquema de traducción recursivo por la izquierda (en concreto las reglas recursivas por la izquierda son las 10, 11, 13 y 14):

0	p $\rightarrow$ ds ss	{ $p{t} = { n => 0, ds => $ds{t}, ss => $ss{t} } }
1	p $\rightarrow$ ss	{ $p{t} = { n => 1, ss => $ss{t} } }
2	ds $\rightarrow$ d ';' ds	{ $ds{t} = { n => 2, d => $d{t}, ; => ';', ds => $ds{t} } }
3	ds $\rightarrow$ d ';'	{ $ds{t} = { n => 3, d => $d{t} ; => ';' } }
4	d $\rightarrow$ INT il	{ $d{t} = { n => 4, INT => 'INT', il >$il{t} } }
5	d $\rightarrow$ STRING il	{ $d{t} = { n => 5, STRING => 'STRING', il >$il{t} } }
6	ss $\rightarrow$ s ';' ss	{ $ss{t} = { n => 6, s => $s{t}, ; => ';' ss => $ss{t} } }
7	ss $\rightarrow$ s	{ $ss{t} = { n => 7, s => $s{t} } }
8	s $\rightarrow$ ID '=' e	{ $s{t} = { n => 8, ID => $ID{v}, = => '=', e => $e{t} } }
9	s $\rightarrow$ P e	{ $s{t} = { n => 9, P => 'P', e => $e{t} } }
10	e $\rightarrow$ e1 '+' t	{ $e{t} = { n => 10, e => $e1{t}, + => '+', t => $t{t} } }
11	e $\rightarrow$ e1 '-' t	{ $e{t} = { n => 11, e => $e1{t}, - => '-', t => $t{t} } }
12	e $\rightarrow$ t	{ $e{t} = { n => 12, t => $t{t} } }
13	t $\rightarrow$ t1 '*' f	{ $t{t} = { n => 13, t => $t1{t}, * => '*', f => $f{t} } }
14	t $\rightarrow$ t '/' f	{ $t{t} = { n => 14, t => $t1{t}, / => '/', f => $f{t} } }
15	t $\rightarrow$ f	{ $t{t} = { n => 15, f => $f{t} } }
16	f $\rightarrow$ '(' e ')'	{ $f{t} = { n => 16, ( => '(', e => $e{t}, ) => ')' } }
17	f $\rightarrow$ ID	{ $f{t} = { n => 17, ID => $ID{v} } }
18	f $\rightarrow$ NUM	{ $f{t} = { n => 18, NUM => $NUM{v} } }
19	f $\rightarrow$ STR	{ $f{t} = { n => 19, STR => $STR{v} } }
20	il $\rightarrow$ ID ',' il	{ $il{t} = { n => 20, ID => $ID{v}, ',' => ',', il => $il{t} } }
21	il $\rightarrow$ ID	{ $il{t} = { n => 21, ID => $ID{v} } }
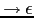
22	s $\rightarrow \epsilon$	{ $s{t} = { n => 22, s => '' }}

Por razones de espacio hemos abreviado los nombres de las variables. El atributo t (por tree) es una referencia a un hash. La entrada n contiene el número de la regla en juego. Hay una entrada por símbolo en la parte derecha. El atributo v de ID es la cadena asociada con el identificador. El atributo v de NUM es el valor numérico asociado con el terminal. Se trata de, siguiendo la metodología explicada en la sección anterior, construir un analizador descendente predictivo recursivo que sea equivalente al esquema anterior. Elimine la recursión por la izquierda. Traslade las acciones a los lugares convenientes en el nuevo esquema e introduzca los atributos heredados que sean necesarios. Genere pruebas siguiendo la metodología explicada en la sección 4.4.1. ¡Note que el árbol que debe producir es el de la gramática inicial, ¡No el de la gramática transformada!

Sig: Árbol de Análisis Abstracto Sup: Recursión por la Izquierda Ant: Ejercicio Err: Si hallas una errata ...